菱形的性质和判定（初中数学菱形的性质和判定）

大家好，这里是周老师数学课堂，欢迎来到头条号学习！

今天继续分享的特殊的平行四边形——菱形，首先学习菱形的基本知识:

一.菱形的性质

二.菱形的判定

三.菱形甚础题

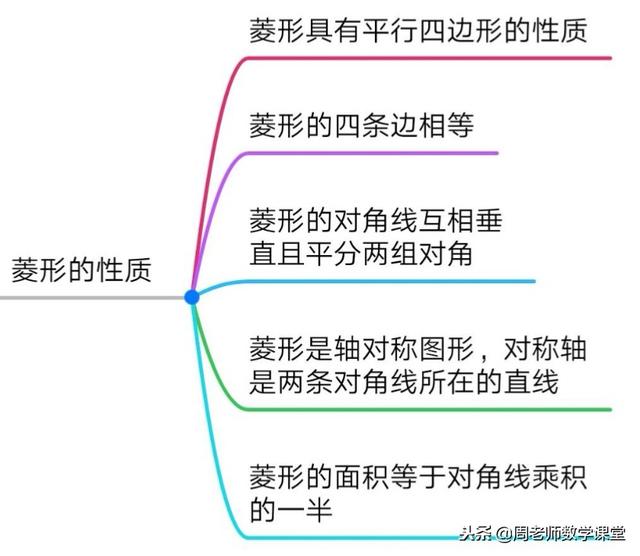
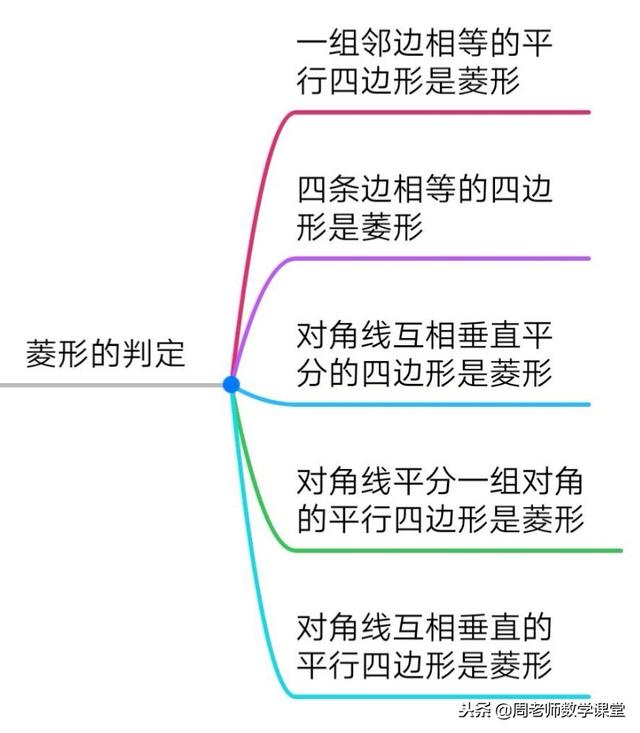
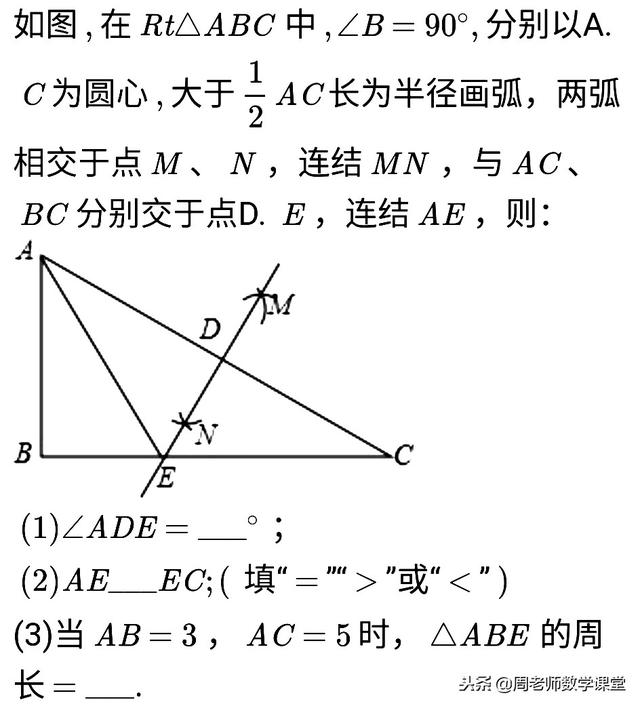
[解析]

⑴ 由作图可知，MN是线段AC的垂直平分线，故可得出结论；

⑵ 根据线段垂直平分线的性质即可得出结论；

⑶ 先根据勾股定理求出BC的长，进而可得出结论.

[解答]

四.菱形性质与判定综合题

如图，已知△ABC是等腰三角形，顶角∠BAC=α(α<60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转a到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF.

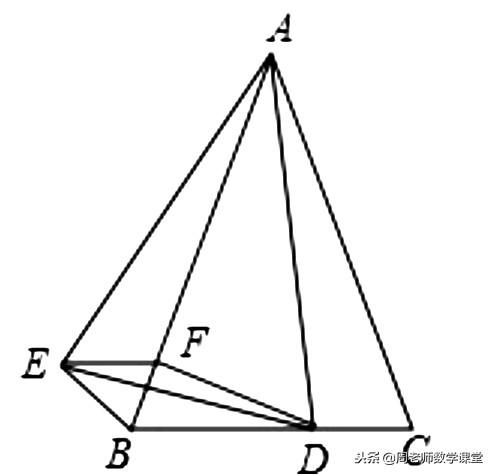
⑴ 求证：BE=CD；

⑵ 若AD丄BC，试判断四边形BDFE的形状，并给出证明。

[解析]

⑴ 根据旋转可得∠BAE=∠CAD，从而SAS证明△ACDS2△ABE,得出答案BE=CD;

⑵ 由AD//BC，SAS可△ACD≌△ABE≌△ABD,从而得出BE=BD=CD,∠EBF=∠DBF,再由EF//BC,∠DBF=∠EFB,从而得出∠EBF=∠EFB,则EB=EF，证明得出四边形BDFE为菱形.

[解答]

[小结]

上题和矩形一样，菱形也是中考考查的重点，除了考查菱形的判定和性质之外，利用对角线求菱形的面积也是重点，希望同学们加强练习，掌握好菱形的知识。

今天的分享就到这里，欢迎大家在评论区留下您的思路，让我们共同讨论，也许您的方法是最棒的。喜欢文章记得分享哦！