相似三角形培优题技巧（用好轴对称的性质）

大家好，这里是周老师数学课堂，欢迎来到百家号学习！

如图，将三角形纸片ABC沿直线DE折叠后，使得点B与点A重合，折痕分别交BC,AB于点D，E.如果AC=5cm,△ADC的周长为17cm，那么

BC的长为（ ）。

A.7cm

B.10cm

C.12cm

D.22cm

[解答]

解:将△ABC沿直线DE折叠后，使得点B与点A重合，

∴AD=BD,

∴AC=5cm，△ADC的周长为17cm，

∴AD CD=BC=17-5=12(cm).

故选:C.

[解析]

上题利用翻折变换的性质，根据题意得出AD=BD，进而利用AD CD=BC得出即可.

[知识清单:折叠的性质与运用]

⑴ 翻折变换(折叠问题）实质上就是轴对称变换.折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.

⑵在解决实际问题时，对于折叠较为复杂的问题可以实际操作图形的折叠，这样便于找到图形间的关系.首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件。

解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案.我们运用方程解决时，应认真审题，设出正确的未知数。

如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN ∠ANM的度数为（ ）。

A.130°

B.120°

C.110°

D.100°

[解答]

作A关于BC和CD的对称点A′，A”，连接A'A"，交BC于M，交CD于N，则A'A”即为△AMN的周长最小值。作DA延长线AH，

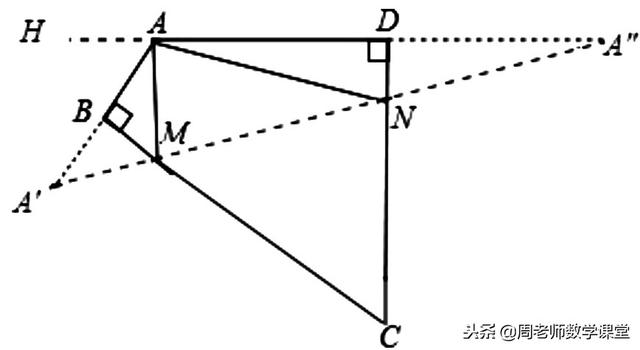
∵∠DAB=120°，

∴∠HAA'=60°，

∴∠AA'M ∠A"=∠HAA'=60°,

∵∠MA'A=∠MAA',∠NAD=∠A",

且∠MA'A ∠MAA'=∠AMN,

∠NAD ∠A"=∠ANM,

∴∠AMN ∠ANM

=∠MA'A ∠MAA' NAD ∠A"

=2(∠AA′M ∠A")=2×60°=120°，

故选:B.

[解析]

根据题意要使△AMN的周长最小，即利用点的对称性，让三角形的三边在同一直线上，作出A关于BC和CD的对称点A'，A”，即可得出∠AAM ∠A"=∠HAA'=60°,进而得出∠AMN ∠ANM=2(∠AAM ∠A")即可得出答案.

[知识点清单:最短路线问题]

解几条线段之和最小(短)类问题，一般是运用轴对称变换将处于直线同侧的点转化为直线异侧的点，从而把两条线段的位置关系转换，再根据两点之间线段最短或垂线段最短来确定方案，使两条线段之和转化为一条线段。